1 feszültség vonalak
§2.1 feszültséget vonalak. Áramlási intenzitása vektor.
Az elektromos mező egyedileg meghatározható, ha a nagyságát (modulus) és irány vektort minden egyes pont a térben. Ezt meg lehet tenni, ha abban a térben, hogy végezzen az úgynevezett feszültség vonal (távvezeték) elektromos térben.
Ilyen vonalat húztunk úgy, hogy az érintő a feszültségi vonal egybeesik az irányt a vektor


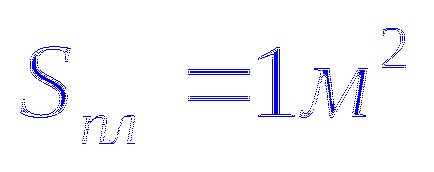

A pont-töltés mező vonalak sugárirányú vonalak. Pozitív díjak - így a díjat a végtelen, a negatív - jön a töltést végtelenig.
H
Így a sorok számát N kimenő A díj mindig állandó marad. azaz
Ez azt jelenti, hogy a vonalak a feszültség kivételével bárhol a töltés nem kezdődik és vége: a pozitív töltés megy a végtelenségig, a negatív érkező végtelenbe és végződnek a díjat. Ezen a téren nem metszik egymást. Ez a vektor vonalakat tulajdonság közös az összes elektrosztatikus mezők mezők által létrehozott álló díjak rendszere.
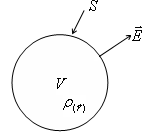
Tekintsünk egy felületén, amely egy S. elektromos mező

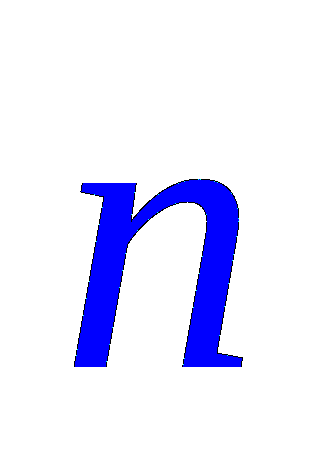
A vonalak száma (1)
Expression (1) az úgynevezett áramlási vektor a felületen keresztül S.
Takarmány vektor - skalár mennyiség.
A jelentését a fluxus vektor E - száma erővonalak, amelyek behatolnak ezen felület S.
E
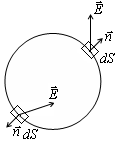

Az expressziós vektor az úgynevezett átfolyó a zárt felület.
§2.2. Gauss-tétel.
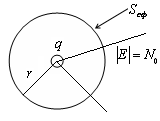
Az előző részben, megállapítottuk, hogy az egy pont töltés áramlik át a körét (zárt felület):
Ha a felület egy „ránc”, a feszültségi vonalat mindig a határt keresztező felületek páratlan számú alkalommal, és így bármely körülvevő felület töltés
Ha van egy adózási rendszert körül tetszőleges zárt felületre S alapján a szuperpozíció elve alapján felírható:
Expression (2) az úgynevezett Gauss-tétel: áramlási vektor révén egy tetszőleges felület megegyezik az algebrai összege a díjak korlátozódik a felületen belül osztva.
Különösen, ha nincs díj belsejében S, vagy;
Ha a töltés eloszlik a felületen folyamatos a térfogatsűrűsége. akkor a teljes töltés és belül S. áramot (* 2)
T
Gauss-tétel lehet kifejezni differenciális formában. Ehhez használja a tétel Ostogradskogo-Gauss, amely összeköti az integrál a zárt felület S az integrál a kötet V. Ez a korlátozott felülete S.
Ha megad egy szimbolikus vektor operátor nabla:
És végül megkapjuk:
Kapcsolat (3) van a differenciális alakja Gauss tétel.
Egyenletek (2) és (* 2), (3) - az egyik alapvető elektrosztatika arányok. Gauss-tétel érvényes a következő okok miatt:
A kölcsönhatás erő közötti pont díjak fordítottan arányos a távolság négyzetével közötti díjakat.
A központi karakter a kölcsönhatás erők.
lineáris szuperpozíció hatások miatt a különböző díjakat.
Mély fizikai jelentősége Gauss tétel. A természetben van elektromos töltések és azok forrása az elektromos mező.
Amint azt az alábbiakban bemutatjuk (2) összefüggés (* 2), (3) tartalmazza az úgynevezett Maxwell egyenletek klasszikus elektrodinamika, mint az első egyenlet.
§2.3. Alkalmazása Gauss-törvény, hogy megtalálják az elektrosztatikus mező.
Mert az elektrosztatikus feltöltődés, amelynek szférikus és hengeres szimmetria, Gauss tétel lehetővé teszi számunkra, hogy meghatározzuk a területen a díj egy egyszerűbb módon, mint ha számoltuk közvetlenül Coulomb-törvény és a szuperpozíció elve.
a) mező a végtelen szál egyenletesen töltött.
A lineáris töltéssűrűség:
P
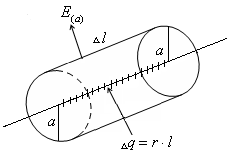

Mi ugyanahhoz az eredményhez alapján a Gauss-tétel. Nyilvánvaló, hogy a feszültséget merőleges az izzószál. A távolból egy a végtelen. Így a probléma van, hengeres szimmetria tengely körül egybeesik a menet.
Mi körülveszik a szál henger a sugarú és hosszát. Mivel a vektor merőleges a hengerpalást, a erővonalak Eprohodyat csak az oldalsó felületen. Alkalmazása Gauss-tétel kapjuk:
Megvan ugyanazt az eredményt.
b
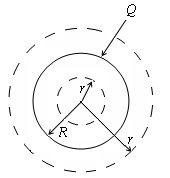
Tedd a fém golyó töltés Q töltés egyenletesen oszlik el a gömb felületén. Bent a labda nincs díj. Miután leírtuk a a gömb középpontja körül a gömb tetszőleges r sugarú Így a mező belsejében a fém gömb függetlenül attól, hogy szilárd vagy üreges hiányzik. Hasonlóképpen, alkalmazva a Gauss-tétel pont körén kívül (r> R), azt találjuk: A területen kívüli területen egybeesik területén ponttöltés Q. központjában található a gömb. A felszín közelében (ezen kívül) is könnyen meghatározható, ha E r = R tegye az utolsó kifejezés. Ezután - a felületi töltés sűrűség a gömbön. és Ez a kifejezés az E érvényes minden a töltött fém vázban. Meg kell jegyezni, hogy a fém test bármilyen alakú különböző pontokat a test felületén. c) Most tekintsünk egy végtelen sík, amelyen töltés egyenletesen oszlik felületi sűrűsége. Találunk intenzitását E egy tetszőleges távolságra repülő. Könnyen belátható, hogy a vektor merőleges a síkra.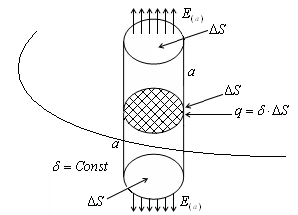
Mi választjuk ki egy tetszőleges terület sík.
Construct alapján egy függőleges henger, magassága síkja felett és alatt. A végén a henger, és lép ki a henger. Ezért vektor áramlás halad csak végein keresztül. Alkalmazzuk a Gauss-tétel:
Így az elektromos mező független a távolban egy minden pontján tér felett és alatt síkja azonos :. Egy ilyen mező homogénnek nevezzük.
g) Határozzuk meg az E elektromos tér és belül egyenletesen által felszámított kötet egy gömb sugara R.
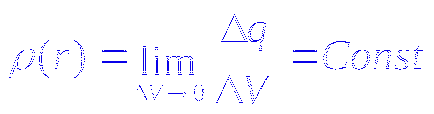
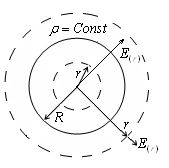
Leírjuk a gömb középpontja körül a gömb tetszőleges r sugarú A Gauss-tétel: Ha az r Így a mező által felszámított térfogatú gömb egybeesik a területén ponttöltés Q. központjában a gömb. W d) A mező két párhuzamos sík, megbízott ellentétes töltéseket. P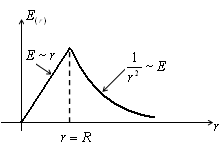
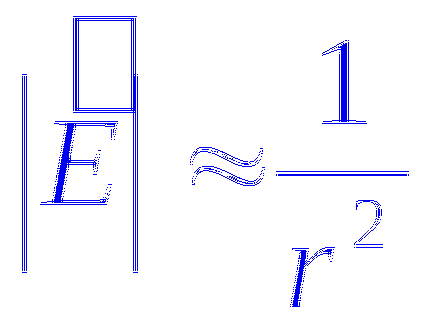
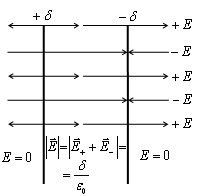

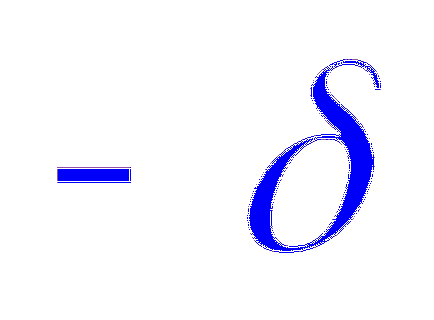

Megjegyzés. Ha figyelembe vesszük a valós elrendezése két párhuzamos lemezek közötti távolság, amely sokkal kisebb, mint a méret a lemezek (planáris kondenzátor), az elektromos mező belsejében a mellékelt lemez, és annak intenzitása
f) Hasonlóképpen az elektromos mező számítják mezhdukoaksialnymi (koaxiális) egyenletesen töltött a hosszával lineáris sűrűsége radiusamii henger.
az
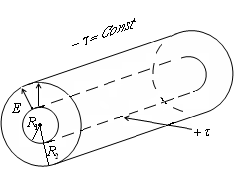
r a távolság a henger tengelyével.
Amikor a végső hossza a henger, egy ilyen készülék az úgynevezett hengeres kondenzátor.
g) A mező a két koncentrikus gömböket radiusamii.
E
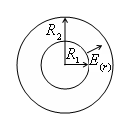


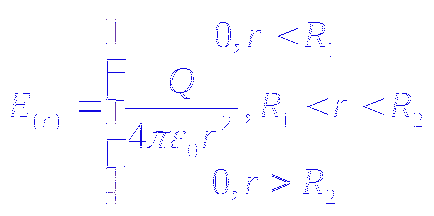
Egy ilyen készülék az úgynevezett egy gömb alakú kondenzátort.