Az egyenes vonalú mozgás egy anyagi pont

Tápszerek származnak egyenes vonalú mozgás egy háromutas mozgás feladat -, ismert koordinátáit, attól függően, hogy az idő; Egy ismert gyorsulás az idő függvényében, és a gyorsulás a koordináta. Tekinthető egyenes vonalú egyenletes egyenes vonalú egyenletesen gyorsuló mozgás.

Alapképletek egyenes vonalú mozgás

Legyen egy anyagi pont mozog a vonal mentén. Továbbá, és jelzi a helyzetét és sebességét az a pont a kezdeti időben.
Ha a törvény változásai meghatározott koordinátáit időben:
.
differenciáló koordináta az idő, megkapjuk a sebesség és a gyorsulás a lényeg:
;
.

Hadd tudja a függőség a gyorsulás ideje:
.
Ezután, attól függően, a sebesség és pozíció időről időre által meghatározott képlet:
(1);
(2);
(3);
(4).

Tegyük fel, hogy tudjuk, hogy a gyorsulás függ a koordinátákat:
.
Ezután a sebesség függvényében a koordináták a következők:
(5).
A koordináta idő kerül meghatározásra implicit formában:
(6).

Egyenes vonalú egyenletes mozgás:
;
;
.

Egyenes vonalú egyenletesen gyorsuló mozgás:
;
;
;
.

Az itt közölt képletekkel lehet használni nem csak egyenes vonalú mozgás, hanem egyes esetekben a görbe vonalú mozgás. Például háromdimenziós mozgás derékszögű koordinátarendszerben. ha a mozgás tengelye mentén független az értékeket a kiemelkedések a többi tengely. Ezután az (1) - (6) biztosítja a kiálló értékek függően tengelyen.

Továbbá, ezek a képletek esetén alkalmazandó vezetés előre meghatározott pálya mentén a mozgás során a természetes folyamat munkát. Csak itt úgy viselkedik, mint egy koordináta az ív úthossz mérve a kiválasztott eredetű. Ezután, ahelyett, hogy a kiemelkedések és kell szubsztituált és - vetülete a sebesség és a gyorsulás a kiválasztott irányba az érintő a pályához.

Az egyenes vonalú mozgás ismert koordinátáinak, attól függően, hogy az idő

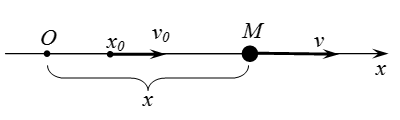
Vegyük azt az esetet, amikor az anyagi pont mozog egy egyenes vonal. Úgy döntünk, egy koordináta-rendszert és annak eredete egy tetszőleges helyen. Tengely mentén irányul vonal a mozgás egy pont. Ezután a pont pozícióját egyedileg határozza meg az egységes koordináta.

Ha a törvény megváltozik beállított koordináta az idő.
.
majd differenciáló idő tekintetében. Találunk a változás üteme a törvény:
.
Amikor a pont mozog a pozitív irányba (balról jobbra az ábrán). Amikor a pont mozog a negatív tengely irányában (az ábrán jobbról balra).

Differenciálás az idő függvényében a sebességet, azt látjuk, a törvény változása gyorsulás:
.
Mivel a sorban nincs görbület görbületi sugara a pálya tekinthető végtelenül nagy. Ezután a gyorsulás egyenlő nullával:






.
Ez a pont a tangenciális gyorsulás (érintő)
.
Ez egészen természetes, hiszen mind a sebesség és a gyorsulás a pont érintő irányú pályára - a vonal, amely mentén a mozgás történik.
Ha ugyanaz a jel (vagyis mind a pozitív vagy mindkettő negatív), a modulus növekszik sebesség (sebessége növekszik abszolút értékben). Ha különböző jelek, akkor a modulus csökken sebesség (fordulatszám csökken abszolút értékben).

Lineáris mozgás egy bizonyos gyorsulás

Gyorsulás, időfüggő

Hadd tudja a törvény változása gyorsulás ideje:
.
A mi feladatunk az, hogy megtaláljuk a törvény a változás és a változás a koordinátáit idő:
;
.

Alkalmazza a képlet:
.
Ez egy elsőrendű differenciálegyenlet elkülöníthető változókat. Osztozunk változók és integrálja:
;
.
Itt - a folyamatos integráció. Ez azt mutatja, hogy csak az ismert gyorsulás az idő függvényében, akkor nem egyedi azonosítására a függőség mértéke időről időre. Kaptunk egy csomó sebesség jogszabályi változások, amelyek különböznek egymástól tetszőleges konstans. Ahhoz, hogy megtalálja a változás üteme minket a törvény, amit fel kell tennünk egy másik jelentése. Általában ez az érték az érték a sebesség a kezdeti időben. Ehhez jár a határozatlan integrál definíciója:
.
Hagyja, - a lényeg a sebesség a kezdeti időben. Mi helyettesíti.
;
;
.
Így joggal sebessége változik időről időre a formája:
(1).

Hasonlóképpen, a koordináták határozzák meg a törvény időbeli változása.
.
(2).
Itt - az érték a kezdeti időben.

Behelyettesítve (1) a (2).

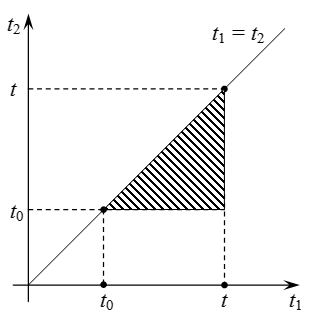
A régió az integráció a kettős integrál.

Ha megváltoztatja a sorrendben az integráció a kettős integrál, megkapjuk:

Így van a következő képlet:
(3);
(4).

A gyorsulás-függő koordinátákat

Tegyük fel most, hogy tudjuk a törvény változásának gyorsulása a koordinátákat:
.
Meg kell oldani a differenciálegyenletet:
.
Ez differenciálegyenlet nem tartalmaz független változó kifejezetten. Általános eljárás megoldására ilyen egyenletek tartják az oldalon „magasabb rendű differenciálegyenletek, amelyek nem tartalmazzák a független változó kifejezetten”. E szerint a módszer, úgy véljük, hogy a funkció a.
;
.
Osztozunk változók és integrálja:
;
;
;
.
Figyelembe négyzetgyöke kell jegyezni, hogy a sebesség egyaránt lehet pozitív és negatív. Egy rövid távolságra a lényeg. jel előjele határozza meg az állandó. Azonban, ha a gyorsulást ellentétes irányú a sebesség, a lényeg sebesség nullára csökken, és a mozgás irányát megfordítjuk. Ezért a helyes jel, plusz vagy mínusz, kiválasztva a figyelmet egy bizonyos mozgás.
(5).
Elején a mozgás
.

Most határozzuk meg a függőség a koordinátákat az idő. A differenciálegyenlet a koordinátái a következő formában:
.
Ez differenciálegyenlet elkülöníthető változókat. Osztozunk változók és integrálja:
(6).
Ez az egyenlet határozza meg a függőség a koordinátáit idő hallgatólagosan.

Egységes lineáris

Alkalmazzuk a fenti eredményeket az esetben egyenes vonalú egyenletes mozgás. Ebben az esetben a gyorsulás
.
Képlet alapján (1) és (2) találunk:
;
. Azaz, a sebesség állandó, és koordinálja a lineáris idő függvényében. (5) és (6) ugyanazt az eredményt adja.

Egyenes vonalú egyenletesen gyorsuló mozgás

Most tekintsük az egyenes vonalú egyenletesen gyorsuló mozgás.
Ebben az esetben a gyorsulás állandó:
.
Képlet alapján (1) és (2) találunk:
;

Ha alkalmazzuk az (5), megkapjuk a sebesség függvényében a koordináták:
.

Lineáris mozgás vektor formában

Az így kapott képlet képviseli vektor formában. Ehhez szaporodnak elég meghatározó egyenletek. és a készülék vektor (egységvektor). tengelyének irányába.

Ezután a sugara vektort a pont, a sebesség és a gyorsulás vektorok a formában:
;
;
.