Az eljárás a problémák megoldására a szuperpozíció elve

Home | Rólunk | visszacsatolás

1.Prochitat feladat; írd le az összes beállított értékek fizikai mennyiségek és átalakítani őket, hogy az SI-rendszerben.

· Az ábrán ábrázolják töltéseloszlásbeli hogy készítsen egy területen;

· Válassza ki a koordináta-rendszerben, figyelembe véve a szimmetria a problémát;

· Megjelölésére távolságok, amelyek ahhoz szükségesek, hogy megoldja azt a problémát, és hogy felhívja a vektorok térerő által generált minden elosztási díj az érdekes pont.

3. Írja be a képlet a feszültséget moduli mezők egyes díjak egy adott ponton.

4. A tervezés erőssége minden vektor a koordinátatengelyt, hogy megtalálják a vetülete a teljes intenzitását vektor az egyes tengelyeken. Ismerve a teljes vetülete a vektor a koordinátatengelyeken Ex. Ey és az EZ. tudjuk számítani a teljes egység vektor alkalmazásával a Pitagorasz-tétel.

Példák problémák megoldására a számítás az elektromos mezőket alapján a szuperpozíció elve

Találja meg az elektromos tér A és B pontok
(Lásd. Ábra.) Fekvő függőleges felezővonal közötti pont díjak q1 = 8 NC és nC q2 = -6, amelyek vákuumban. A távolság a díjak r = 10 cm, AB = 4 cm, e = 1.

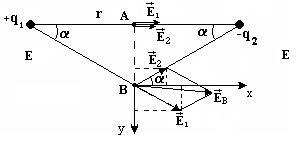
Az ábrán a megállapodás a díjak és a A és B pontok, amelyekre meg kell találnunk a térerő, és a választott koordináta-rendszerben ábrázolt.

a) Az A. pont jön létre, a két pont díjak Q1 és Q2. A definíció szerint a térerősség - az az erő, amellyel a töltés mezőt előállító egység a pozitív ponttöltés elhelyezett, az A pont, így a feszültség vektorba, amely ugyanabba az irányba. A teljes feszültség összege a térerősség az egyes díjak

vagy vetülete a tengelyen OX

Írunk a képlet a nagysága a térerősség pont díjak Q1 és Q2 a pont:

És, hogy a pont:

b). B pontban vektorok és 2a irányul szögben egymáshoz, és a modulok a vektorok nem ugyanaz, mert értéke Q1 és Q2 különböző díjakat.

Írunk a képlet a nagysága a térerőt Q1 Q2 és pont díjak pont B:

Ezeknek a vektoroknak mindegyike ad nyúlvány mindkét tengelyen:

Az előrejelzések teljes intenzitását vektor B pontnál lesz egyenlő:

Most már lehetséges a képlet a Pitagorasz-tétel, hogy kiszámolja a modulusa a vektor az elektromos mező keletkezik a B pont díjak Q1 és Q2. .

Az összes kifejezést nyert csinál algebrai átalakításokat, megkapjuk a végső kifejezése kiszámításához a kívánt mennyiséget:

Kiszámoljuk a számértéke a teljes mezőt pont B:

Megjegyzés. Bizonyos esetekben, amikor a döntés oka, hogy a meglehetősen nehézkes algebrai átalakításokat, tudjuk elvégezni számítások során a probléma megoldásának. Így volt lehetséges, hogy nem, és hogy megoldja ezt a problémát.

A: Az elektromos térerősség az pont az,
EA = 50,4 kV / m és irányul a töltés a töltés Q1 Q2. B pontban, a feszültség egyenlő U = 24,1 kV / m és annak irányát mutatja.

3. példa 1 Két hosszú menetes hasonló töltésű távközzel r1 = 10cm egymástól. A lineáris töltéssűrűség azonos, és egyenlő = 10mkKl / m.

Megtalálni a nagyságát és irányát a kapott térerősség A pont, minden egyes szál távoli távolságból a = 10cm.

Elektrosztatikus mezők által generált különböző eloszlások díjak vannak kialakítva a szuperpozíció elve minden ponton a térben. Mivel a szimmetria a probléma, hogy egy rajzot, forgalomba a szál merőleges a rajz síkjára. Egy pont távolítani mindkét szálon olyan távolságban egy = r1 .Poluchili oldalú háromszög. Ahhoz, hogy megtalálja az irányt a vektor térerősség keletkezik a pont számít minden egyes szál ebbe a tárgyalás díj pont „1”, és meghatározza, hogy a fonalak mezők hatnak ezt a díjat. Mivel a szálak pozitív töltésű, akkor taszítják a teszt töltés és a vektor és a fog irányulni, mint látható. Vector teljes térerősség szerint a szuperpozíció elve, található a paralelogramma szabály.

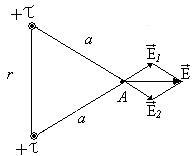
A kölcsönhatás erősségét ezen töltésű szálak függ a közöttük levő távolság, így a művelet az elektrosztatikus térerő kell kiszámítani a szerves, amikor kiterjesztett szálak.

1) Látható, hogy jobbra mutat, és a modul megtalálható, mint:

2) A kölcsönhatás erősségét töltött szálak függ a köztük lévő távolság. Minden szál létrehoz egy mezőt, és ezen a területen hat a díjat egy másik téma. - a térerő az első szál.

-az erő egységnyi hossza a második szál:

A munka ennek erőt lehet kiszámítani:

Vegyük az integrál a funkciót. Minden állandók vegye ki az integrál jel és szerezzen táblázatos integrál, ami megegyezik a természetes logaritmusa az érvelés.

Mi helyettesítheti a határait integráció és végül megkapjuk:

Az adatok a probléma, megkapjuk a numerikus választ

A pozitív töltés a q = 5 × 10 -8 Kd egyenletesen elosztott finom drót semiring sugara R = 20 cm. Annak megállapításához, a E térerősségű középpontjában a semiring.

q = 5 × 10 -8 Kd;

Elemzés és döntés. Ebben a feladatot, a mező által termelt töltés q, elosztva a vékony fél-gyűrűk R sugarú A lineáris töltéssűrűség :. Egy ilyen esetben nem lehet közvetlenül használni a képlet a térerősség ponttöltés vagy töltött végtelen izzószál. Ezt a problémát meg lehet oldani a szuperpozíció elve. Osszuk a teljes útmutatót, nagyon kis parcellákon hosszúságú dl. minden egyes elszámolási díj dq = t × dl. Egy ilyen töltés lehet tekinteni, mint egy pont értéke, és a térerősség a töltés képlet szerint kiszámított

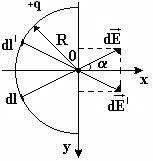
Az ábra mutatja a választás a koordináta-tengelyek és a vektor mezőben. keletkező O felelős .Given szimmetriáját a probléma, amely a referencia-pont koordinátarendszer társított az O pont, a központ a félgyűrűt és továbbítja a koordinátatengelyek, mint látható.

Vetítjük a vektor a koordinátatengelyeken:

Az is látszik az szimmetria, hogy minden egyes elemi töltés dq van elrendezve szimmetrikusan tengelyéhez képest OX töltés dq ¢. A vetítés a térerősség ezeket a díjakat az y tengely hogy zéró egyáltalán szögei.

Így meg kell találni csak a teljes vetülete a vektor az x tengelyen. Magától értetődő, hogy abban az esetben egy folytonos eloszlású a díjat kell helyettesíteni összegzése integráció teljes hosszában a huzal, amelyen a töltés.

A integrandus tartalmaz két változó L és. Tekintettel arra, hogy és dl = Rd egy, cserélje az integrációs változó, és szerezzen

Az ábra azt mutatja, hogy. a.

A: A térerősség a gyűrű középpontjába egyenlő 7,2 kV / m.

Az ábra azt mutatja, egy töltött végtelen sík felületével síkja töltés SCLC s = 40 / m 2, és ugyanolyan töltésű gyöngy tömegű m = l g és töltés q = 1 NC. Mi a szög a síkra egy szál, amelyen a labda lóg?

A díj a síkban a területen. Úgy működik, három labda erőt ábrán látható. Írunk a feltétele a labda egyensúly.

Vetítjük a kapott egyenletet a koordináta tengelyekkel:

Megoldása az egyenletrendszert, megkapjuk Fel. = Mg × TGA. .

Másrészt, Fel. = QE. ahol E - elektromos mező által létrehozott egy végtelen síkot.

A kapott egyenletrendszert már

Field végtelen sík a következőképpen fejezhető ki:

Ebben az esetben a díj, és a gép a levegőben, azaz e = 1.

tga = 0,2259 »0226

A: A szál a sík szöge a = 13 0.