B) területének kiszámítására az ábra által határolt

.

B) területének kiszámítására az ábra vonallal körülhatárolt. . . .

Határozat. Először végezze el a rajz:

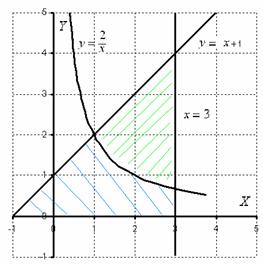
Az ábra, amely egy olyan terület, meg kell találnunk egy árnyékos kék (nézd meg alaposan a feltétel - mi a szám korlátozott). A gyakorlatban azonban, mivel a figyelmetlenség gyakran a kérdés, hogy meg kell találni a terület az ábra, amit az árnyalt zöld!

Ez a példa is hasznos, hogy megvizsgálta a területet az ábra két határozott integrálok. valóban:

1) található egy szegmens fölött a tengelye a vonal grafikon;

2) A szegmens fölött tengelye a grafikon egy hiperbola.

Nyilvánvaló, hogy a terület lehet (és kell) add on, így:

Találunk meghatározott vonalak keresztezési pontot. Ehhez megoldjuk az egyenletrendszert:

Ahhoz, hogy megtalálja az abszcissza adott vonalai metszéspontjai az egyenlet megoldásához:

Így, az adatsort egy parabola és az egyenes vonal metszéspontjai A (-2; 0), B (4; 6).

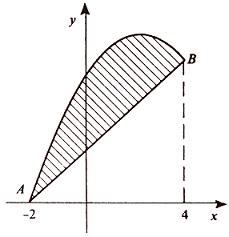
Ezek a vonalak egy zárt forma, a terület kiszámítása a fenti képlet:

Szerint a Newton-Leibniz lelet:

a) Meg kell találni a határozott integrál

Így a kívánt szerves egyenlő 6.

8. példa Keresse meg a határozatlan integrál:

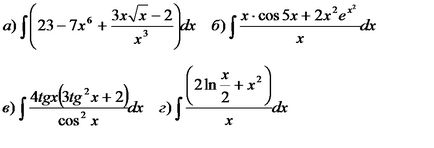
A megoldási példák tulajdonságainak használata határozatlan integrálok, táblázata integrálok, amely magában foglalta a képlet a szerves lineáris függvénye az érvelés, és közvetlen integrálását a helyettesítési módszer.

b) befejezése termwise részlege az integrandus, kapjuk:

d) használjuk a szubsztitúció:

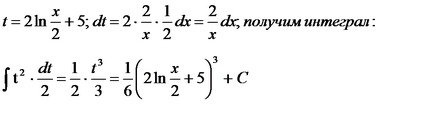
d) igénybe helyettesítés:

1) Számítsuk határozott integrálok:

A számítástechnikai határozott integrálok segítségével alaptételének képletű

. Előállítás primitív függvény F (x) elvégzi vagy közvetlenül, vagy annak helyettesítésére.

1) műveleteket végezze összeadás, kivonás, szorzás, osztás a komplex számok algebrai formában.

Először átalakítsa a második szám, és az értékeket a fokok az imaginárius egység. i 18 = i 16 = i 2 + i 2 16 2 = 1i = -1, i 15 = i 12 + 3 12 = i 3 i 3 = i = -i, Z2 = -2 + 5i

Mi végre műveleteket szám:

a) Van egy sor színes gyöngyök, amelyek közül 5 kék, piros és zöld 3 2. Ball véletlenszerűen extraháljuk 4. Annak a valószínűsége, hogy többek között az órák gyöngyök 2 kék, 1 piros és 1 zöld.

Ahhoz, hogy meghatározzuk a valószínűsége, hogy egy véletlen esemény fogja használni a klasszikus képlet. ahol n - a szám minden lehetséges kimenetelt, m- esetek száma kedvező megjelenése esetén. A probléma ezen értékek találhatók révén kombinációk.

b) A kártyákat szét az ábécé alkotják a „panoráma”. Kártyák és véletlenszerűen keverjük egy kártyát 5 eltávolítjuk, szóló őket abban a sorrendben extrakciós. Annak a valószínűsége, hogy fogja elkészíteni a szó „újszerű”.

Ebben a feladatban, akkor a termék független véletlen események

És - szerzés a szó „romantika”;

B1 - Kivonat az első kártyát a „p” betű;

B2 - kivonására a második kártya az „O” betűvel; stb

P (A) = P (B1). P (B2). P (B3). P (B4). P (B5) =