Hogyan lehet bővíteni a száma prímszám 2

Lemezszámokban papíron (fent). Alatt számos felhívni két átlós vonal - egy irányítani a megfelelő, és a második - a bal oldalon. Vagy írjon az alábbi telefonszámon, és felhívni két átlós vonal fölé. Példa: feküdt a prímfaktorizáció a 315. 315. /. \

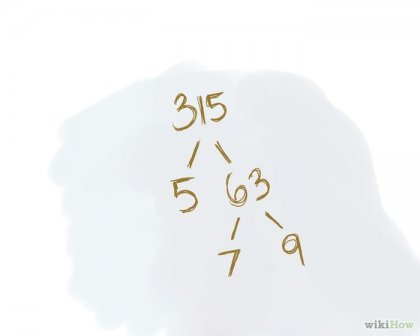
Mert a két szorzók írd néhány tényező. Egy pár multiplikátor - két szám, amelynek a termék megegyezik az eredeti számot. Ne írjon szorzókat prímszám. Példa. 315 /. \. 5. 63 / \. 7. 9

Keresés bármely két tényező egy adott számot. Egy pár multiplikátor - két szám, melynek terméke megegyezik az eredeti szám. [1] Ez a két tényező kell írni az ferde vonalak. Választhat bármilyen pár tényező. A végeredmény nem függ a választás. Megjegyzendő, hogy ha ez a párok száma szorzók nem (kivéve az 1. és magát a számot), ez egy prímszám, és azt nem lehet számításba. Példa. 315 /. \. 5. 63

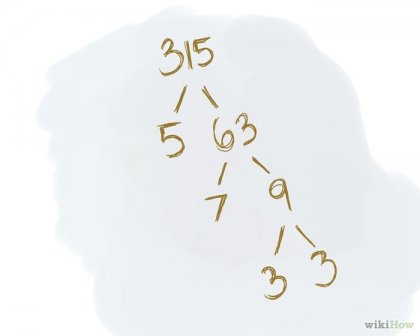
Ismételje meg a folyamatot, amíg nem marad egyetlen prímszám (prímszám). Prímszám - egy szám, amely osztható csak önmagában és 1. Folytatás felhívni az átlós vonalak és rögzítse egy pár szorzók amíg a találkozás prímszám. Felhívjuk figyelmét, hogy a fa szerkezetét, a szám a szorzók 1 ne legyen. Példa. 315 /. \. 5. 63. / .. \. 7. 9. / .. \. 3. 3

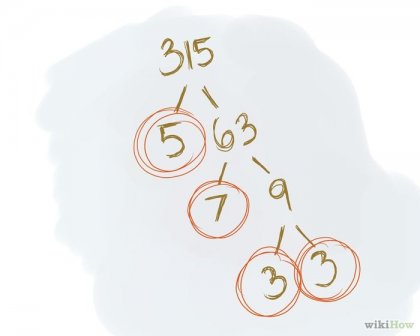
Amint szembesül egy prímszám (prímfaktorizáció) válasszuk ki a (kör vagy aláhúzás), hogy ne veszítsen elágazó fa struktúra tényezők. Példa: prímtényezőit számok 5, 7, 3, 315. 3. /. \. 5. 63. / .. \. 7. 9. / .. \. 3. 3. Alternatív: át az elsődleges tényező az egyes következő szint a fa struktúra és tényezőket, így nem veszíti el - Az összes tényezőt fog elhelyezkedni a legalacsonyabb szinten. [2] Példa. 315 /. \. 5. 63. /. / .. \. 5. 7. 9. /. /. / .. \ 5. 7. 3. 3

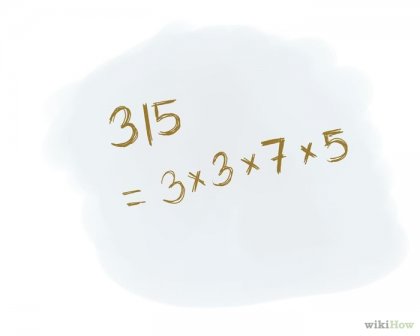
Válasz meg van írva, mint a termék elsődleges tényező. [3] Ha a tanár kell írni a választ a formájában egy fa struktúra szorzók, hagyja a dolgokat, ahogy vannak; különben rögzíti a válasz a következő: Példa: 5 * 7 * 3 * 3

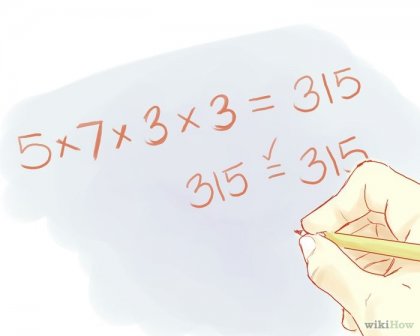
Ellenőrizze a választ. Szorozzuk meg a kapott prímosztók, és akkor kap az eredeti számot. Példa: 5 * 7 * 3 * 3 = 315

Felbomlása után számokat prímszám írd le az összes elsődleges tényező az egyes számot. Ezután válasszuk ki, vagy írjon az összes közös faktorok (tényezők vannak jelen az egyes listája elsődleges tényezők). A listák nincsenek közös tényezők, akkor GCD = 1. példa: közös prímtényezője szám 195 és 260 a számok 5 és 13.

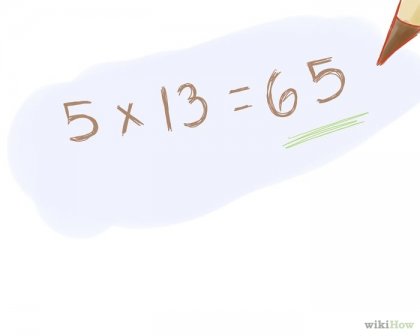
Szorzás közös tényezők. [4] Ha ezek a számok több közös elsődleges tényező, hogy kell szorozni, hogy megtalálják a GCD. Ha ezek a számok csak egy közös elsődleges tényező, ez egyenlő a GCD. Példa: általános tényezők szám 195 és 260 5 és 13 Szorozzuk őket, és kap 5 * 13 = 65

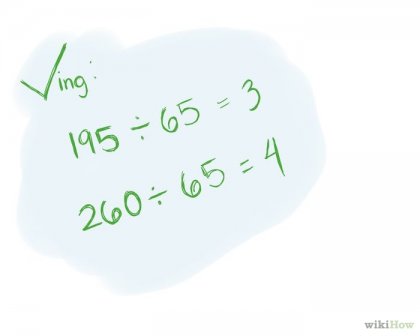
Írja le a választ. Dupla ellenőrizze a válasz adatokat számát elosztjuk megtalálta a GCD. Ha a számok alá GBR egyenletesen, akkor a válasz helyes. Példa: GCD számok 195 és 260 egyenlő 65. 195/65 = 3. 260/65 = 4.

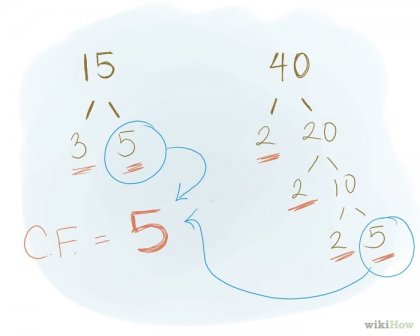
Felbomlása után számokat prímszám írd le az összes elsődleges tényező az egyes számot. Ezután válasszuk ki, vagy írjon az összes közös vonás. Felhívjuk figyelmét, hogy ha kapnak három (vagy több) a számos közös tényező jelen kell lennie a listán a tényezők legalább két szám az adatok (és nem minden tényező szerepel). Nem tartalmazzák a kettős szorzók. Például, ha a tényezők listája első szorzó 2 kétszer van jelen, és a lista a tényezők második szorzó 2 csak egy alkalommal, akkor meg kell jegyeznünk egy 2 az első listában, és a 2 a második (azaz a második 2 az első listában nem tekinti ). Példa: általános tényezők szám 15 és 40 csak az 5-ös szám.

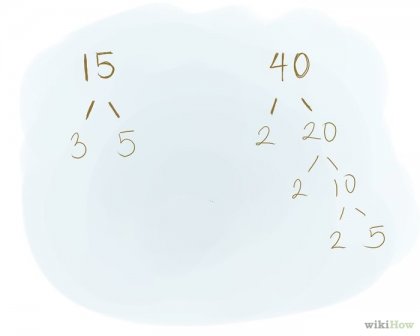
Ahhoz, hogy megtalálja a legkisebb közös többszörös (LCM) két vagy több számot kell lebontani ezen számokat elsődleges tényező. Ehhez használja a fent leírt módszer. Meg kell, hogy hozzon létre egy fa struktúra az egyes tényezők. Ehhez használja a fent leírt módszer. NOC - a legkisebb szám, amely osztható adott számot. Példa: Határozza meg a legkisebb közös többszöröse 15 és 40 15. / .. \. 3. 5 prímtényezőjét száma 15: 3, 5. 40. /. \. 5. 8. / .. \. 2. 4. / \. 2. 2 prímtényezőjét 40 a számok 5, 2, 2, 2.

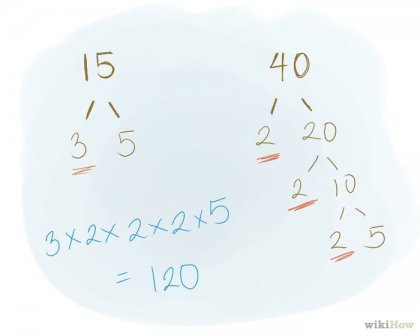
Szorozzuk meg a közös tényező, és minden olyan tényező, amely nem gyakori. Ez figyelembe veszi mindazokat a tényezőket, amelyek nem gyakori. A fenti példában a második 2 az első listában figyelembe kell venni. Az általános szorzó kezelik, mint egy számot. Példa: A közös tényező az a szám, 5. Sokszorozó amelyek nem megosztott, a szám lesz 3, 2, 2, 2. Ezért kell szorozni: 5 * 3 * 2 * 2 * 2 = 120.

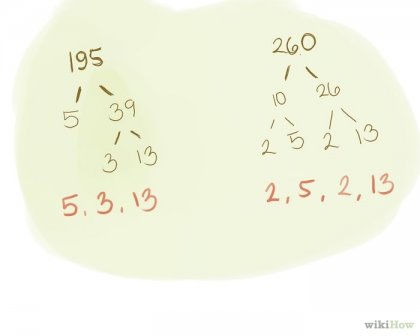
Megtalálása a legnagyobb közös osztója (GCD) két vagy több számot kell lebontani ezen számokat elsődleges tényező. Ehhez használja a fent leírt módszer. Meg kell, hogy hozzon létre egy fa struktúra az egyes tényezők. Ehhez használja a fent leírt módszer. NOD - a legnagyobb szám, amely egyenletesen osztja minden adott számot. Példa: megtalálni a legnagyobb közös osztója a szám 195 és 260 195. /. \. 5. 39. /. \. 3. 13 prímtényezőjét 195 van a 3, 5, 260. 13. /. \. 10. 26. /. \ ... / .. \ 0,2. 5. 2. 13 prímtényezőjét 260 számok: 2, 2, 5, 13.

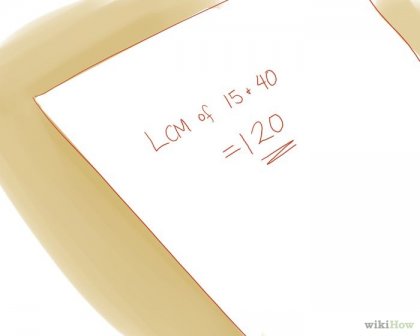
Írja le a választ. Példa számok NOC 15 és 40 RANS 120.

256338 256339 256340 256341 256342 256343 256344 256345 256346 256347 256348 256349 256350 256351