Hogyan számoljuk ki a területet az ábra segítségével a határozott integrál

Home | Rólunk | visszacsatolás

Mi jár, hogy fontolja alkalmazása integrálszámítás. Ebben a leckében fogjuk megvitatni a típus, és a leggyakoribb probléma a terület kiszámításával síkidom segítségével a határozott integrál. Végül, minden keres értelmet magasabb matematika -, de találni. Sosem lehet tudni. Majd meg kell megközelíteni az élet itt a külvárosi területen elemi függvények és megtalálni a területen útján határozott integrál.

Ahhoz, hogy sikeresen elsajátítani az anyagot, akkor köteles:

1) Értse meg a határozatlan integrál legalább az átlagos szintet. Így vízforraló először megismerni a leckét határozatlan integrál. Ilyen megoldásokat.

2) Ahhoz, hogy alkalmazni Alaptételének képlet, és kiszámítja a határozott integrál. Létrehozza meleg és baráti kapcsolatokat egyes integrálok határozott integrál lehet az oldalon. Ilyen megoldásokat. Task „területének kiszámítására a határozott integrál” mindig magában foglalja az építési rajzot. Ezért fontos kérdés lesz a tudás és készségek a műszaki rajzok. Legalább akkor képesnek kell lennie, hogy építsenek egy egyenes vonal, parabola és hiperbola.

Kezdjük egy íves trapéz. Görbe vonalú trapéz - síkidom által határolt grafikon y = f (x), a tengely OX és a vonalak x = a; X = b.

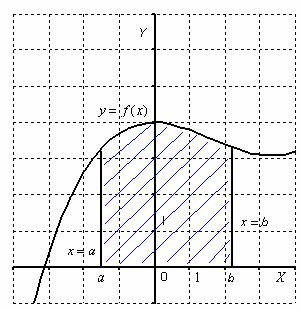
A területet a görbe vonalú trapéz számszerűen egyenlő a határozott integrál

Bármilyen határozott integrál (ami létezik) van egy nagyon szép geometriai jelentés. A lecke határozott integrál. Ilyen megoldásokat mondtuk, hogy a határozott integrál - ezt a számot. És most itt az ideje bevallani, még egy hasznos tény. Az szempontjából a geometria a határozott integrál - egy szóközt. Azaz, a határozott integrál (ha létezik) geometriailag területnek felel meg az egyes számok. Tekintsük a határozott integrál

egy görbét definiál a síkban (kívánt esetben ez lehet levonni), és a határozott integrál számszerűen egyenlő a megfelelő terület görbe vonalú trapéz.

Számoljuk ki a területet az ábra által határolt vonal. . . .

Ez egy tipikus készítmény a feladat. A legfontosabb döntés pillanatában - az építőiparban a rajzon. Sőt, a rajznak megfelelően épült.

Az építőiparban a rajz, ajánlom a következő eljárás: első, hogy egy jobb a vonalak (ha van ilyen), és csak ezután - parabola, hiperbola, grafikák egyéb funkciók. A technika pontonkénti építési megtalálható referenciaanyag grafikonok és tulajdonságait az elemi függvények. Ott lehet találni nagyon hasznos tekintetében a leckét - hogyan lehet gyorsan építeni egy parabola.

Ebben a feladatban a megoldás nézhet.

Végezze rajz (megjegyezzük, hogy az egyenlet y = 0 meghatározza az OX tengely):

Hatch görbe trapéz nem, itt nyilvánvaló, hogy milyen a szóban forgó területen. A döntés így folytatja:

A [-2; 1] a grafikon y = x 2 + 2 felett található osyuOX. ezért:

Azok, akik vannak nehézségek a számítás határozott integrál és használata Newton-Leibniz formula

Lásd az előadás határozott integrál. Ilyen megoldásokat. Ha a munkát végzik, mindig hasznos, hogy nézd meg a rajzot, és kitalálni, hogy az igazi válasz kiderült. Ebben az esetben a „szemmel” számít a sejtek száma a rajzon - nos, mintegy 9 gépelt, hasonlóan az igazság. Egyértelmű, hogy ha kiderült, mondjuk, a válasz 20 négyzetméter egység, akkor egyértelmű, hogy valahol hiba - a vizsgált szám 20 sejtek nyilvánvalóan nem illik, egy tucat erők. Ha a válasz nemleges kiderült, a feladat is megoldható-e.

Számítsuk ki a területet az ábra által határolt xy = 4, X = 2, x = 4 és OX tengely.

Ez egy példa a független megoldásokat. Teljes körű megoldásokat és válaszokat a végén a leckét.

Mi van, ha a görbe vonalú trapéz alatt osyuOX?

Számítsuk ki a területet az ábra által határolt vonalak y = e - x. X = 1, és a koordináta-tengelyek.

Megoldás: rajz:

Ha a görbe vonalú trapéz terheli az OX tengelyen. hogy a területen megtalálható a következő képlettel:

Ebben az esetben:

Figyelem! Ne tévesszük össze a kétféle probléma:

1) Ha a rendszer megkérdezi, hogy megoldja a határozott integrál nélkül geometriai értelemben negatív is lehet.

2) Ha a rendszer kéri, hogy megtalálják a terület az ábrán a határozott integrál, a terület mindig pozitív! Éppen ezért csak tekinteni képlet jelenik meg negatív.

A gyakorlatban, gyakran egy alak, és elhelyezve a felső és az alsó felében, és így, az elemi iskolai zadachek fordulnak egy értelmes példákat.

Mekkora területű síkidom által határolt vonal y = 2x - x 2 y = -x.

Megoldás: Először is, el kell végezni a rajzot. Az építőiparban a rajzot a problémák a térségben a leginkább érdekli metszi a vonalakat. Találunk a metszéspont a parabola y = 2x - x 2 és egyenes y = -x. Ezt meg lehet tenni két módon. Az első módszer - analitikai. Mi megoldjuk az egyenletet:

Ennélfogva, az alsó határ az integráció, a = 0, a felső határa az integráció b = 3. A legtöbb előnyös és építeni gyorsabb vonal pontonkénti, az integrációs határok vizsgálják, mintha „magukat”. Azonban az analitikai módszert kell találni a határok néha még mindig kell alkalmazni, ha például a gráf elég nagy, vagy potochennoe építkezés során nem merült fel a határait integráció (ami lehet tört vagy irracionális). Visszatérünk a feladatunk: építeni egy racionális első sorban, majd a parabola. Végezze rajz:

Ismét az épület a pontonkénti határait integráció gyakran tisztázni „avtomatomaticheski”.

Most dolgozik képlet:

Ha az intervallum [a; b] folytonos f (x) nagyobb vagy egyenlő, mint egy folytonos függvény g (x), a megfelelő terület az ábra megtalálható a következő képlettel:

Nincs többé szükség arra gondolni, ahol ez a szám - felett tengelyt vagy tengely alatti, de fontos, hogy mi a fenti ábra (másikhoz képest táblázatot), és amely - az alábbiakban.

Ebben a példában, nyilvánvaló, hogy a [0; 3] parabola található egyenes felett, és így a 2x - x 2 kell vonni -x.

Alkatrészek az oldatot a következőképpen nézhet ki:

Kedvelt ábra által határolt parabola y = 2x - x 2 a fenti, és Y = -x egyenes alulról.

A [0; 3] 2x - x 2 ≥ -x. A általános képletnek megfelelő:

Tény, hogy az iskolai képlet területének íves trapéz alsó felében (lásd példa №3.) - egy speciális esete a formula

Mivel OX tengelye adott egyenlet y = 0, egy görbét g (x) alatt helyezkedik el a tengelyen OX. az

És most néhány példát egyedi megoldások

Keresse meg a területet az ábra által határolt

Keresse meg a területet az ábra által határolt

Ennek során a problémák megoldásában a számítás terület segítségével a határozott integrál megtörténik néha szórakoztató esemény. Rajz megfelelően rendezni - jobb, de véletlenül ... Találd meg a területet a rossz számok.

Ezután egy igazi eset:

Számoljuk ki a területet az ábra által határolt vonal. . . .

Először végezze el a rajz:

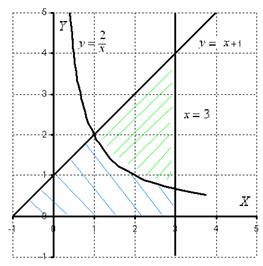
Az ábra, amely egy olyan terület, meg kell találnunk egy árnyékos kék (nézd meg alaposan a feltétel - mi a szám korlátozott). A gyakorlatban azonban, mivel a gondatlanság, gyakran úgy, hogy meg kell találni a terület az ábra, amit az árnyalt zöld!

Ez a példa is hasznos, hogy megvizsgálta a területet az ábra két határozott integrálok. valóban:

1) intervallumon [-1; 1] a OX tengely az a vonal grafikon y = x + 1;

2) intervallumon [1; 3] a OX tengely hiperbola grafikon y = (2 / X).

Nyilvánvaló, hogy a terület lehet (és kell) add on, így:

Számoljuk ki a területet az ábra által határolt

Mi képviseli az egyenlet az „iskola”, mint

és végezze el a pontonkénti rajz:

Az ábrából kitűnik, hogy a felső határ a „jó»: b = 1.

De mi is az alsó határ. Nyilvánvaló, hogy ez nem egy egész, de mit?

Talán a = (- 1/3)? De hol van a garancia arra, hogy a rajz kerül végrehajtásra tökéletes pontossággal, az is lehet, hogy a = (- 1/4). És ha nem baj ábrázoljuk?

Ilyen esetekben meg kell időt tölteni, és adja meg a határait integráció analitikusan.

Találunk a metszéspontja a grafikonok

Ahhoz, hogy ezt elérjük, az egyenlet megoldásához:

Következésképpen, a = (- 1/3).

Egy további megoldás triviális. A lényeg, hogy ne vesszenek el a helyettesítések és a jelek. A számítások nem nagyon egyszerű. az intervallum

általános képletű:

Összefoglalva a lecke, úgy a két feladat nehéz.

Számoljuk ki a területet az ábra által határolt

Megoldás: Tegyük képviseli ez a szám a rajzban.

Pont-pont építése a rajz kell tudni a megjelenése egy szinuszhullám. Általában hasznos tudni, hogy a menetrendek az összes elemi függvények, valamint néhány érték a szinusz. Ezek megtalálhatók a táblázatban az értékek trigonometrikus függvények. Bizonyos esetekben (például ez) lehetővé tette az építőiparban a rajzra, ahol elvileg kell helyesen jelenik grafika és korlátait integráció.

A külső nincsenek problémák az integráció, követik közvetlenül a feltétel:

- „X” változik nulláról „pisilni”. Azt, hogy egy újabb döntést:

A [0; π] a grafikon y = sin x 3 felett található a tengely OX. ezért:

(1) Mivel az integrált szinusz és koszinusz páratlan erejét, lehetséges, hogy a lecke integrálok trigonometrikus függvények. Leszorítják a sinus.

(2) Az általános trigonometrikus identitás

(3) elvégzi a változás a változó t = cos x. akkor:

Új integrációs folyamat szakaszai:

Ki nem rossz dolog helyettesítések, lépjen osztály helyettesítő módszer a határozatlan integrál. Ez nem nagyon világos csere algoritmus egy határozott integrál, keresse fel a határozott integrál. Ilyen megoldásokat.

(4) Itt használjuk a tulajdonságait a határozott integrál

szûkíti az integráció a „szokásos” érdekében

Számoljuk ki a területet az ábra által határolt

Ez egy példa a független megoldásokat. A teljes megoldás, és a választ az alábbiakban.

Vegyünk egy érdekes példát Arccotangent:

Számoljuk ki a területet az ábra által határolt

és a koordináta-tengely. Komplett megoldás nem. Helyes válasz:

2. példa: Oldat: rajz:

Az intervallum [2; 4] a grafikon y = 4 / X fölött helyezkedik OX tengelyen, tehát:

Megjegyzés: A probléma megtalálni a területek tanárok gyakran kell rögzíteni a válasz nem csak pontos, hanem különösen kb.

5. példa Megoldás: rajz:

A intervallum [-1; 3]. . általános képletű:

6. példa: Megoldás: Végezze rajz.

A intervallum [1; 3] (4-x) ≥ (3 / X), az általános képletnek felel meg:

10. példa: Oldat: Mi képviseli ez a szám a rajzon:

A grafikonon a szegmens található a tengely fölé. ezért:

Megjegyzés: Figyeljük meg, hogy a szerves venni a tangens a kocka, már használta a fő következménye trigonometrikus azonosságok

Továbbá, a integrálok a módszer összeadásával funkciók jel alatt az eltérés (lehet használni csere a határozott integrál, de a döntés hosszabb lesz).