izometrikus

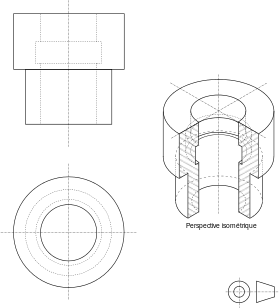
Négyszögletű izometrikus nézetben részleteket a „perselyt” készül alapján a merőleges vetülete

Izometrikus nézet használt mérnöki és CAD szerkesztési építési vizuális képet részletesebben a rajzon. valamint a számítógépes játékok háromdimenziós objektumok és panorámával.

Meg kell jegyezni, hogy a párhuzamos vetítés. fajokat, amelyekre axonometrikus és beleértve izometrikus vetítés, is osztva ortogonális (merőleges) a vetület irányára merőleges a vetítési sík és ferde. közötti szög irányába, és a gép más, mint egy jobbra. Szerint a szovjet szabványok (lásd. Lent) axonometrikus ábrázolásban lehet ortogonális és ferde [1]. Ennek eredményeként, a nyugati szabványok izometrikus nézete szűkebben meghatározott és, amellett, hogy az egyenlő a tengelyek skála, magában foglalja a feltétel az egyenlő szögek a 120 ° közötti bármely két kiálló tengely. A félreértések elkerülése érdekében, a továbbiakban, hacsak másként nem jelezzük, csak szögletes izometrikus vetítés értünk izometrikus vetítés.

Szabványos izometrikus vetülete [1] szerkesztése

A téglalap alakú (ortogonális) izometrikus nézet szerkesztése

A téglalap alakú izometrikus axonometrikus tengelyek képeznek azok között egy 120 ° -os szögben, Z „tengely függőlegesen. Torzítás együtthatók (k x. K y. K z, k_, k_>) van számértéke február 3 ≈ 0. 82 >> \ kb 0,82>. Általában a konstrukciók, hogy megkönnyítse izometrikus vetítés működnek torzítás nélkül a tengelyek, azaz torzítás tényező határozza meg, hogy 1 ebben az esetben, egy lineáris növekedését méretének 0. 1 82 ≈ 1. 22> \ kb 1,22> alkalommal.

Ferde frontális izometrikus nézet szerkesztése

Z „tengely függőlegesen, a szög közötti tengely X” és Z „90 ° -kal egyenlő, Y” tengely hajlásszöge 135 ° (120 °, és hagyjuk 150 °) a Z „tengelye.

Az elülső izometrikus nézet mentén végrehajtott tengelyek X „Y” és Z „torzítás nélkül.

Curves párhuzamos a frontális síkban vetített torzítás nélkül.

Vízszintes ferde izometrikus nézet szerkesztése

Z „tengely függőlegesen, a Z tengely” és Y-tengely szög 120 ° (135 °, és hagyjuk 150 °), miközben a szög között a tengelyek X »és Y« 90 ° -kal egyenlő.

Vízszintes izometrikus vetítés működnek torzítás nélkül a tengelyek X „Y” és Z”.

Curves párhuzamos vízszintes sík [2] Az előrejelzések torzítás nélkül.

Meg kell jegyezni, hogy mivel az ortogonális háromszögletű lehetetlen kapcsolja úgy, hogy két, a szélei egymásra merőleges, és a harmadik széle nincs kivetítve, hogy látható legyen, hogy egy pont, az összes a nyúlványok, ami azt mutatja, mind a három tengely, de a rajz közötti szög k -n két - sor (itt ez a második, a harmadik a fenti), szigorúan véve, a show „valamit, ami nem történt meg.”

Szerencsére az emberi szem meglehetősen sikeresen korrigálja az ilyen hibák képviseletét valós objektumok, és mert lehetővé tette az egyszerűség kedvéért az építés a rajzon.

Izometrikus nézetben az objektum lehet elő megtekintésével irányba úgy, hogy a bezárt szög a vetítési tengelyen x. y. és Z azonosak voltak, és egyenlő a 120 °. Például, ha vesszük a kocka, akkor lehet, hogy végre küldő pillantást az egyik kocka arcok, majd fordult a kocka ± 45 ° a függőleges tengely körül, és ± arcsin (tan 30 °) ≈ 35,264 ° vízszintes tengely körül. Megjegyzés: Az ábrán izometrikus vetítés kocka körvonala képez szabályos hatszög - minden éle egyenlő hosszú és minden oldala egyenlő területet.

Egy másik módja, hogy szemléltesse izometrikus vetítés vizsgálni a formát egy köbös helyiség felső szöge az irányt a látvány egy ellentétes alsó sarokban. X-tengely irányul ferdén lefelé, és a jobb oldali, a y tengely - egyenesen felfelé - lefelé és átlósan balra, z tengely. Mélység is tükröződik a kép magasságát. Rajzolt vonalak tengelyek mentén van egy 120 ° -os szögben közöttük.

Jelenleg 8 különböző lehetőségek egyre izometrikus nézetben, attól függően, hogy mit néz oktáns megfigyelő. Izometrikus átalakulási pontja egy x. y. z> a háromdimenziós térben a b pont x. y> síkban nézve az első oktáns lehet matematikailag leírható egy rotációs mátrix a következőképpen. Először is, amint azt a szakaszt megjelenítés. végzett rotációs egy vízszintes tengely körül (itt, x) a α = arcsin (tan 30 °) ≈ 35.264 ° és egy függőleges tengely körül (itt, y) a β = 45 °:

A többi hét lehetséges típusai kap viszont, hogy az ellenkező oldalon és / vagy inverziót irányába tekintetét. [3]

Korlátozások perspektivikus nézete szerkesztése

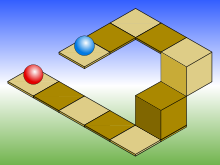
Izometrikus rajz egy kék labda két szint fölött a piros

Mint más típusú párhuzamos kiemelkedések. tárgyak terv nem nagyobb vagy kisebb zoomolás vagy távol a megfigyelő. Ez akkor hasznos, építészeti rajzok és kényelmesen a sprite-orientált számítógépes játékok. de, ellentétben a ígéretes (központi) vetítés. Ez vezet egyfajta görbület, mint az emberi szem vagy fotó munka másképp.

Azt is könnyen vezethet a helyzetekben, ahol a mélység és a magasság nem lehet értékelni, mint az az ábrán látható, hogy a jobb oldalon. Ez izometrikus rajz egy kék labda két szint fölött a piros, de lehetetlen, hogy ha itt most csak a bal fele a képet. Ha a vetítés, amelyen a kék labdát, meghosszabbítja egy négyzet, akkor lenne pontosan mellett a tér, ami egy piros labdát, ami egy optikai csalódás. ha mindkét golyó azonos szinten.

Egy további sajátos problémája az izometrikus vetítés - a nehéz meghatározni, hogy melyik oldalon az objektum figyelhető meg. Hiányában a árnyékok és a tárgyak, amelyek viszonylag merőleges, és arányos, nehéz meghatározni, hogy melyik oldalán van a felső, alsó vagy oldalsó. Ez annak köszönhető, hogy a körülbelül azonos méretű és területe kiemelkedések a tárgy.

A legtöbb modern számítógépes játékok elkerülni, mert az nem perspektivikusan javára hosszú távú háromdimenziós megjelenítésre. A művelet azonban a vetítés optikai illúziókat népszerűbb művészeti - mint például a munka egy sor „lehetetlen építészet” Escher. Falls (1961) - egy jó példa, amelyben a szerkezet elsősorban izometrikus, míg a halvány háttér használ perspektivikus vetítés. További előny, hogy a kidolgozása a kezdők is könnyen építeni szögek 60 °, amelyek csak vonalzót és iránytű.

Izometrikus vetítés a videojátékok és a pixel art szerkesztése

Ábra TV szinte-izometrikus pixel art. A pixel mintázat látható, hogy az aránya 2: 1

A területen a számítógépes játékok és a pixel art perspektivikus képe már nagyon népszerű, mivel a könnyedség, amellyel a két dimenziós sprite és csempézett grafika lehetne használni, hogy képviselje a háromdimenziós játék környezetben - például a mozgás során a játéktér objektumok nem változik a mérete a számítógép nem szükséges méretarányos sprite vagy számítások elvégzéséhez szükséges, hogy szimulálja a vizuális szempontból. Ez lehetővé tette a régi 8-bites és 16-bites játék rendszerek (és később, hordozható játék rendszerek), hogy könnyen egy nagyméretű háromdimenziós térben. Bár zavar a mélységgel (lásd. Fent), néha olyan probléma, jó játék design képes enyhíteni azt. Az Advent a nagyobb teljesítményű grafikus rendszer távlati képe kezdte elveszíteni pozícióikat.

A vetítés a számítógépes játékok általában kissé eltér az „igazi” terv korlátai miatt raszteres grafika - vonalak az x és y tengely nem lenne tiszta pixel minta, ha húzott szögben 30 ° vízszintes. Bár a modern számítógépek probléma megoldásához simítással. korábbi számítógépes grafika nem támogatja eléggé a színpalettát, vagy nem volt elegendő feldolgozási teljesítmény futtatni. Ehelyett használható egy része a pixel minta 2: 1 egy rajzolt tengely irányú x és y. ahol ezek tengelyei szöget arctg 0,5 ≈ 26.565 ° a vízszinteshez képest. (Játék rendszerek nem négyzet alakú pixel lenne, azonban vezethet más sarkok, beleértve a teljesen izometrikus [4]). Mivel itt a három szög tengelyei közötti (116,565 °, 116,565 °, 126,87 °) egyenlő csak két ilyen jellegű vetítési pontosabban jellemzi, mint a variációs dimetric vetítés. A többség azonban a közösség a számítógépes játékok és a rasztergrafika továbbra is hívja ezt a vetületet „izometrikus perspektíva”. Szintén gyakran használt kifejezés „típusú 3/4 (Eng.)” És „2.5D”.

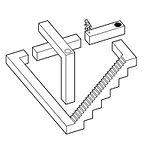
Egy lövés a játék «echochrome»

Egy érdekes példa a használatára a megfigyelt jelenség az izometrikus nézet a játék echochrome (Jap 無限 回廊 Mugen Kairó :.). A szlogen a játék - „Ebben a világban, mit látsz, valósággá válik.” Hogy mit jelent a játék, hogy az illúzió keletkezik, ha ránézünk egy háromdimenziós izometrikus megépített egy bizonyos ponton már nem illúzió. Például, ha megnézi a szintet, hogy a létesülő különböző magasságban, úgy nézett ki, mintha ugyanazon a magasság (cm. A kép vörös és kék golyó az előző részben), a játék akkor tekinthető a azonos magasságban, és az a személy (a játékos) könnyen „átlépni” az egyik oldalon a másik. Aztán, ha viszont a kártya szintet, és nézd meg a szerkezet úgy, hogy jól látható a különbség a magasság, meg lehet érteni, hogy a valóságban az ember „lépcsőzetes” különböző magasságban, az a tény, hogy izometrikus illúzió egy bizonyos ponton vált valóra. Az ábra illusztrációként a keret a játék helyzetet helyén található, a létra tetején, leírható két módja van: az egyik esetben ugyanazon a szinten, mint a platform, amelyen a játékos (lehet meghaladni), míg a másik esetben - alatta (lehetséges, hogy ugrik át fekete lyuk). Mindkét esetben egyidejűleg lehet igaz. Nyilvánvaló, hogy ezt a hatást érjük el hiánya kilátások szempontjából.

Története izometrikus számítógépes játék szerkesztése

Q * bert (1982), az egyik első játék izometrikus grafika

Az első játékok segítségével izometrikus nézet, ügyességi játékok voltak a kezdetektől a 1980-as évek: igen, Q * bert [11] és Zaxxon (. Angol) [12] kiadott 1982-ben. Q * bert mutat statikus piramis, rajzolt izometrikus perspektíva, amelyben a játékosnak kell ugrani-irányított karakter. Zaxxon kínál görgethető izometrikus szinten, amely felett repül a játékos által irányított repülőgép. Egy évvel később, 1983-ban. ügyességi játék Congo Bongo (Eng.) már megjelent [13]. Úgy működik, mint az azonos slot Zaxxon. Ebben a játékban karakter mozog egy nagy izometrikus szinten, amely háromdimenziós kapaszkodók, ereszkedés. Ugyanez kínálják a arcade játék Marble Madness (1984).

• Bogdanov VN Malezhik I. F. Verkhola AP, et al. Referencia nyomtatás. - M. Mechanical Engineering, 1989. - S. 864. - ISBN 5-217-00403-7.
• Frolov S. A. ábrázoló geometria. - 2nd ed. Felülvizsgált. és ext. - M. Mechanical Engineering, 1983. - S. 240.