Kiszámítása területen egy előre meghatározott integrált
Mi jár, hogy fontolja alkalmazása integrálszámítás. Ebben a leckében fogjuk megvitatni a típus, és a leggyakoribb probléma - hogyan kell használni a határozott integrál területének kiszámítására síkidom. Végül keresek jelentését magasabb matematika -, de találni. Sosem lehet tudni. Majd meg kell megközelíteni az élet itt a külvárosi területen elemi függvények és megtalálni a területen útján határozott integrál.
Ahhoz, hogy sikeresen elsajátítani az anyagot, akkor köteles:
1) Értse meg a határozatlan integrál legalább az átlagos szintet. Így vízforraló először megismerni a leckét határozatlan integrál. Ilyen megoldásokat.
2) Ahhoz, hogy alkalmazni Alaptételének képlet, és kiszámítja a határozott integrál. Létrehozza meleg és baráti kapcsolatokat egyes integrálok határozott integrál lehet az oldalon. Ilyen megoldásokat.
Tény, hogy megtalálják a terület az ábrán nem szükséges sok ismeretekkel a határozatlan és határozott integrál. Task „területének kiszámítására a határozott integrál” mindig magában foglalja az építési rajzot. sokkal fontosabb kérdés lesz a tudás és készségek a műszaki rajzok. Ebben az összefüggésben érdemes felfrissíteni alapvető grafikonok elemi függvények és minimumként, képes kialakítani egy egyenes vonal, parabola és hiperbola. Ezt meg lehet tenni (sok - szükséges) egy módszeres anyag grafikonok és tulajdonságait elemi függvények és tárgyak geometriai transzformációk grafikonok.
Valójában, a feladat megtalálni a terület segítségével a határozott integrál minden ismerjük egymást, mivel a középiskolát, és hagyjuk egy kicsit megelőzve a tananyag. Ez a cikk általában nem lenne, de az tény, hogy ez a probléma a 99 100 esetből, amikor egy diák szenved a gyűlölt torony lelkesen mastering során magasabb matematika.
Proceedings of the workshop állapítja meg egyszerűen, részletesen és minimális elmélet.
Kezdjük egy íves trapéz.
A hajlított trapézlemez nevű síkidom által határolt tengely, egyenes, és az intervallum menetrend folytonos függvény, ami nem változik jel ebben az intervallumban. Ne engedd, hogy ez a szám nem éri el az x-tengely:
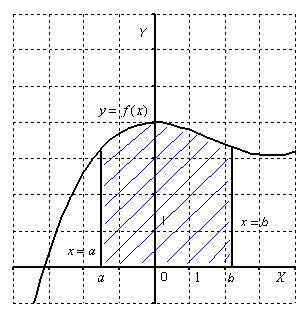
Ezután a területet a görbe vonalú trapéz számszerűen egyenlő a határozott integrál. Bármilyen határozott integrál (ami létezik) van egy nagyon szép geometriai jelentés. A lecke határozott integrál. Példák a megoldások már azt mondta, hogy a határozott integrál - ezt a számot. És most itt az ideje bevallani, még egy hasznos tény. Az szempontjából a geometria a határozott integrál - egy szóközt.
Azaz, a határozott integrál (ha létezik) geometriailag területnek felel meg az egyes számok. Vegyük például a határozott integrál. Az integrandus meghatároz egy síkot görbe fölött fekvő tengelyen (bárki végre a rajz), és a határozott integrál számszerűen egyenlő a megfelelő terület görbe vonalú trapéz.
Számoljuk ki a területet az ábra által határolt ,,,.
Ez egy tipikus készítmény a feladat. Az első és legfontosabb pont megoldások - építési rajz. Sőt, a rajznak megfelelően épült.
Az építőiparban a rajz, ajánlom a következő eljárás: első, hogy egy jobb a vonalak (ha van ilyen), és csak ezután - parabola, hiperbola, grafikák egyéb funkciók. Grafikon funkciók előnyös konstrukció pontonkénti. készülékek pontonkénti építési megtalálható referenciaanyag grafikonok és tulajdonságait az elemi függvények. Ott lehet találni nagyon hasznos tekintetében a leckét - hogyan lehet gyorsan építeni egy parabola.
Ebben a feladatban a megoldás nézhet.
Végezze rajz (megjegyzendő, hogy az egyenlet határozza meg a tengely):
Nem kelnek görbe vonalú trapéz, nyilvánvalóan az egyes területeken kérdéses. A döntés így folytatja:
A grafikonon a szegmens található a tengely fölé. ezért:
Azok, akik vannak nehézségek a számítás határozott integrál és használata Newton-Leibniz formula, lásd az előadás határozott integrál. Ilyen megoldásokat.
Ha a munkát végzik, mindig hasznos, hogy nézd meg a rajzot, és kitalálni, hogy az igazi válasz kiderült. Ebben az esetben a „szemmel” számít a sejtek száma a rajzon - nos, mintegy 9 gépelt, hasonlóan az igazság. Egyértelmű, hogy ha kiderült, mondjuk, a válasz 20 négyzetméter egység, akkor egyértelmű, hogy valahol hiba - a vizsgált szám 20 sejtek nyilvánvalóan nem illik, egy tucat erők. Ha a válasz nemleges kiderült, a feladat is megoldható-e.
Számoljuk ki a területet az ábra vonallal körülhatárolt, és a tengely
Ez egy példa a független megoldásokat. Teljes körű megoldásokat és válaszokat a végén a leckét.
Mi van, ha a görbe vonalú trapéz alatt található tengely?
Számoljuk ki a területet az ábra vonallal körülhatárolt, és a koordináta tengelyek.
Határozat. Végezze rajz:
Ha görbe trapéz alatt elhelyezkedő A tengely (vagy legalábbis nem magasabb, mint egy adott tengely), a terület lehet a következő képlettel:
Ebben az esetben:
Figyelem! Ne tévesszük össze a kétféle probléma:
1) Ha a rendszer megkérdezi, hogy megoldja a határozott integrál nélkül geometriai értelemben negatív is lehet.
2) Ha a rendszer kéri, hogy megtalálják a terület az ábrán a határozott integrál, a terület mindig pozitív! Éppen ezért csak tekinteni képlet jelenik meg negatív.
A gyakorlatban, gyakran egy alak, és elhelyezve a felső és az alsó felében, és így, az elemi iskolai zadachek fordulnak egy értelmes példákat.
Keressen egy lapos terület az ábrán vonallal körülhatárolt.
Határozat. Először el kell végezni a rajzot. Általánosságban elmondható, hogy az építőiparban a rajzot a problémák a térségben a leginkább érdekli metszi a vonalakat. Megtaláljuk a metszéspont a parabola és egy egyenes vonal. Ezt meg lehet tenni két módon. Az első módszer - analitikai. Mi megoldjuk az egyenletet:
Ennélfogva, az alsó határ az integráció, a felső határ az integráció.
Ezáltal jobb, hogy nem használja a lehetőséget.
Ez sokkal jövedelmezőbb és gyorsabb építeni egy sor pont-bölcs, és korlátait integráció kiderült, mintha „magukat.” Technika pontonkénti építési különböző grafikonok tárgyalja részletesen referencia grafikonok és tulajdonságait az elemi függvények. Azonban az analitikai módszert kell találni a határok néha még mindig kell alkalmazni, ha például a gráf elég nagy, vagy potochennoe építkezés során nem merült fel a határait integráció (ami lehet tört vagy irracionális). És ez a példa azt is figyelembe venni.
Visszatérünk a feladatunk: építeni egy racionális első sorban, majd a parabola. Végezze rajz:
Ismét, amikor az építőiparban a pontonkénti határait integráció gyakran kiderült, az „automatikus”.
Most dolgozik formula. Ha az intervallum egy folytonos függvény nagyobb, vagy egyenlő, mint egy folytonos függvény, a terület az ábra által határolt grafikonok funkciók és adatátviteli vonalak, megtalálhatók a következő képlet:
Ott már nem kell gondolni, ahol ez a szám - felett tengelyt vagy tengely alatti, és durván szólva, fontos, amit a fenti táblázat (másikhoz képest táblázatot), és amely - az alábbiakban.
Ebben a példában látható, hogy a szegmens parabola található egyenes felett, és így le kell vonni a
Alkatrészek az oldatot a következőképpen nézhet ki:
Keresek ábra határolt parabola, és egy egyenes vonal, fentről lefelé.
Az intervallum a megfelelő általános képletű:
Tény, hogy az iskolai képlet területének íves trapéz alsó felében (lásd egyszerű példát №3.) - egy speciális esete a képlet. Mivel a tengely következő egyenlet által definiált, egy grafikon a funkció nem található a fenti tengely,
És most néhány példát egyedi megoldások
Keresse meg a területet az ábra vonallal körülhatárolt.
Keresse meg a területet az ábra vonallal körülhatárolt.
Ennek során a problémák megoldásában a számítás terület segítségével a határozott integrál megtörténik néha szórakoztató esemény. Rajz megfelelően rendezni - jobb, de véletlenül találtam a környéken ... nem ez a szám. így többször rendetlen tiéd igazán. Itt egy valós esemény:
Számoljuk ki a területet az ábra által határolt ,,,.
Határozat. Először végezze el a rajz:
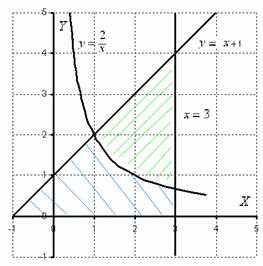
... Ó, hrenovenky rajz jött ki, de úgy tűnik, még mindig olvasható.
Az ábra, amely egy olyan terület, meg kell találnunk egy árnyékos kék (nézd meg alaposan a feltétel - mi a szám korlátozott). A gyakorlatban azonban gyakran van a figyelem hiánya a „glitch”, hogy meg kell találni a területen a szám, amely árnyékos zöld!
Ez a példa is hasznos, hogy megvizsgálta a területet az ábra két határozott integrálok. valóban:
1) található egy szegmens fölött a tengelye a vonal grafikon;
2) A szegmens fölött tengelye a grafikon egy hiperbola.
Nyilvánvaló, hogy a terület lehet (és kell) add on, így:
Azt viszont, hogy még egy értelmes feladat.
Számoljuk ki a területet az ábra által határolt vonalak,
Képviseli az egyenlet „iskola” formában, és végre pontonkénti rajz:
Az ábrából kitűnik, hogy a felső határ a „jó” :.
De mi is az alsó határ. Nyilvánvaló, hogy ez nem egy egész, de mit? Talán? De hol van a garancia arra, hogy a rajz kerül végrehajtásra tökéletes pontossággal, az is lehet, hogy. Vagy gyökér. És ha nem baj ábrázoljuk?
Ilyen esetekben meg kell időt tölteni, és adja meg a határait integráció analitikusan.
Találunk metszéspontjai a vonalat, és a parabola.
Ahhoz, hogy ezt elérjük, az egyenlet megoldásához:
,
Egy további megoldás triviális, még ennél is fontosabb, hogy ne vesszenek el a helyettesítések és jelek, a számítás nem nagyon egyszerű.
Az intervallum a megfelelő általános képletű:
Nos, következtetést a leckét, úgy a két feladat nehéz.
Számoljuk ki a területet az ábra által határolt vonalak,
Határozat. Mi képviseli ez a szám a rajzban.
A fenébe, elfelejtettem, hogy írja alá a menetrend, hanem újra a képet, bocs, nem Hotz. Nem a rajz, a rövid, a mai nap =)
Pont-pont kiépítése szükséges ismerni a megjelenése a szinusz (és általában hasznos tudni jegyzékek minden elemi függvények), valamint néhány érték szinusz, ezek megtalálhatók a trigonometrikus táblázatban. Egyes esetekben (mint ez) megengedett építeni a vázlatos rajz alapján, amelynek elvileg helyesen jelenik meg grafika és korlátait integráció.
A külső nincsenek problémák az integráció, követik közvetlenül a feltétel: - „X” változik nulláról „pisilni”. Azt, hogy egy újabb döntést:
A grafikonon a szegmens fölött helyezkedik el a tengelyen, így:
(1) Mivel az integrált szinusz és koszinusz páratlan hatásköröket lehet megtalálható a leckét integrálok trigonometrikus függvények. Ezt a kifejezést, leszorítják a sinus.
(2) Az általános trigonometrikus identitás
(3) elvégzi a változás a változók, akkor:
Az új határértékek az integráció:
Ki nem rossz dolog helyettesítések, lépjen osztály helyettesítő módszer a határozatlan integrál. Ez nem nagyon világos csere algoritmus egy határozott integrál, keresse fel a határozott integrál. Ilyen megoldásokat.
(4) Itt használjuk a tulajdonságait a határozott integrál, forgalomba határait integráció a „szokásos” érdekében
Számoljuk ki a területet az ábra által határolt vonalak,
Ez egy példa a független megoldásokat. A teljes megoldás és válasz a földszinten.
Itt talán, és az összes alapvető technikákat kell helyet találni. Eltekintve a technikák az integráció, néha szükség van, hogy alkalmazza a képletet integrálás a határozott integrál, ez nem túl nagy nehézséget. Néhány érdekes példa, hogy úgy gondolja, nehéz ... bár ... ív kotangensét fajta soha nem találkoztak:
Számoljuk ki a területet az ábra vonallal körülhatárolt, és a koordináta tengelyek.
Komplett megoldás nem szükséges, mivel te egy kicsit kemény. A helyes válasz fogja mondani. Minden szükséges anyagot a munka a helyszínen is! ;-) És még - miután három éven át, végül megjelent a cikk Terület számítás poláris koordináták, és kiszámítása a területre, ha a vonal határozza parametrikusan.
Megoldások és válaszok:
2. példa: Oldat:
Végezze rajz:
A grafikonon a szegmens fölött helyezkedik el a tengelyen, így:
válaszolni:
Megjegyzés: A probléma megtalálni a területek tanárok gyakran kell rögzíteni a válasz nem csak pontos, hanem különösen kb.
10. példa: Oldat:
Mi képviseli ez a szám a rajzon:
A grafikonon a szegmens fölött helyezkedik el a tengelyen, így:
válaszolni:
Megjegyzés: Figyeljük meg, hogy a szerves venni a tangens a kocka, már használt következtében alapvető trigonometrikus azonosságok. Továbbá az integrálok használtam eljárás összeadásával funkciók alapján eltérés jele (lehet helyettesíteni a határozott integrál, de a döntés, hogy hosszú). Ha nehézségekbe ütközik ezen integrálok, az integrálás fel a leckét a trigonometrikus függvények.
(Ide honlapon)
Minőségi munka nélkül plágium - Zaochnik.com