Példák problémák megoldásához „az térerősség
Ha problémák megoldása fogalmát használva elektromos térerősség először meg kell tudni az (14.8) és (14.9), amely meghatározza a ható erő ellenében az elektromos mező és térerősség egy pont ellenében. Ha a mező által létrehozott számos díjat, majd kiszámítja az intenzitást ezen a ponton meg kell tenni egy rajzot, majd meghatározza a intenzitással, mint a geometriai összege a térerőt.
Probléma 1. Két azonos pozitív ponttöltés távolságban elhelyezett r egymástól vákuumban. Határozzuk meg az elektromos térerősség lévő pont ugyanabban az r távolság ezeket a díjakat.
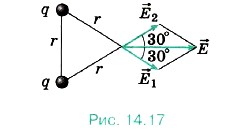
. R e w n e elve szerint a szuperpozíció mező intenzitás megegyezik a kívánt geometriai összege erőssége a mezők által generált minden egyes díjakat (ábra 14,17.): = 1 + 2.
Modulok erősségek hátba területei:
A diagonális a paralelogramma által alkotott vektorok 1 és 2 a intenzitása a kapott mező, a modul, amely a következő:
Probléma 2. A vezetőképes gömb sugara R = 0,2 m, a hordozó töltés q = 1,8 • 10 -4 Cl, található vákuumban. Adjuk meg: 1) a modulusa az elektromos mező a felületén; 2) 1 egység intenzitása az elektromos mező egy olyan ponton a parttól r1 = 10 m-re a központtól a gömb; 3) modul intenzitása 0 közepén a gömb.
R e w n e. Az elektromos teret a feltöltött gömb egybeesik a területén annak ponttöltés. ezért
3) a térerősség bármely ponton belül egy olyan vezetőképes gömb nulla: 0 = E0.
Probléma 3. A homogén elektromos mező intenzitás E0 = 3 kN / C egy pont töltés q = 4 • 10 -10 Cl. Határozzuk meg az elektromos térerősséget a A pont a parttól r = 3 cm-re a ponttöltés. Szegmens összekötő töltés és az A pont merőleges a erővonalait homogén elektromos mező.
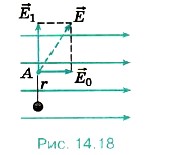
R e w n e. Szerint a szuperpozíció elve alapján, az elektromos térerősséget a pont megegyezik a vektor összege intenzitások egységes mező 0 és mező 1. létre ezen a ponton mentése nélkül elektromos töltés. Ábrán 14.18 mutatja a két vektor és ezek összege. A feladat szerint vektorok 0 és 1 kölcsönösen merőlegesek. A térerő ponttöltés
Ezután az elektromos térerősséget a pont egyenlő:
Feladat 4. A csúcsai egy egyenlő oldalú háromszög, oldalról a = 3 cm három pont díjak q1 = Q2 = 10 -9 Cl, q3 = -2 • 10 -9 Cl. Határozzuk meg az elektromos térerősség a háromszög középpontja az O ponthoz
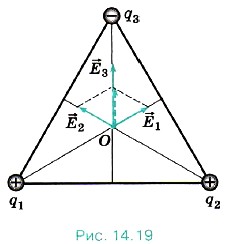
R e w n e elve szerint a szuperpozíció mezők a térerősséget az O pont megegyezik a vektoriális összege térerősségek által generált minden díj külön :. 0 = 1 + 2 + 3, ahol egyébként
Az ábrán a vektorok 14.19 erősségek 1. 2. 3. Először hozzáadjuk a vektorokat az 1. és 2. Amint az az ábrán látható, a bezárt szög ezek a vektorok egyenlő 120 °. Ennélfogva, a vektor összeg modulo modul L1 l és van irányítva, ugyanabban az irányban, mint a vektor 3.
Probléma 5. A távolság a két rögzített díjak q1 = -2 X 10 -9 Cl és q2 = 10 -9 m értéke 1 Cl. Egy bizonyos ponton az elektromos térerősség nulla?
Az 1. és 2. készítette ezeket a díjakat, ugyanabba az irányba „>
R e w n e. Nyilvánvaló, az intervallum között a díjak feszültséget nem lehet nulla, mert az intenzitás a mezők az 1. és 2. A által generált díjak, ugyanabban az irányban (ábra. 14.20).
Következésképpen a térerősség nulla lehet, vagy jobbra vagy balra a díjak a vonalon áthaladó ezeket a díjakat.
Mivel az első töltés egységben nagyobb, mint a második modul, ezen a ponton közelebb kell hozni a második díjat, azaz a. E. Ebben az esetben a jogot a díjak. A távolság a második díjat, hogy az A pont jelöli x. Ezután a feltétellel, hogy | „1 | = „2. felírhatjuk:
-Egyenlet, megkapjuk
Feladatok az önálló döntési
1. függőlegesen lefelé homogén elektromos mező intenzitás 1,3 • 10 5 N / C cseppecske folyékony masszát 2 • 10 -9 g volt egyensúlyban. Határozza meg a töltés cseppek és a felesleges elektronok számát rajta.
2. Egy pont q töltéssel - 10 -9 Cl körülvett gömb alakú héj, egy dielektromos relatív dielektromos ε = 2. A külső héj és a belső sugarak rendre R1 = 5 cm, és R2 = 6 cm Határozza intenzitása E (R) az elektromos mező. attól függően, hogy a távolság a töltés, és felhívni a grafikon ennek a kapcsolatnak.
3. Három koncentrikus gömbök R sugarú, 2R és 3R medve, egyenletesen elosztva a felületi töltések q1 = + 2q, q2 = -q és q3 = + q rendre. Ismeretes, hogy egy pont q töltéssel az R régióban egy elektromos erőteret olyan intenzitással E1 = 63 H / Cl. Mi a térerősség egy pont távol a gömb középpontjától a parttól 2,5R?
A mintákat a munkahelyek USE
A1. B pont van a közepén a szegmens AC. Fix pont díjak és -q -2q található A és C pontok rendre (lásd. Ábra.). Mi a díjat kell elhelyezni a C pontban helyett -2q tölteni az elektromos térerősség a B pontnál nőtt 2-szer?
1) -5q 2) 4q 3) -3q 4) 3q
C2. Ponttöltés q, helyezzük egy koordináta eredetű, létrehoz egy pont intenzitású elektrosztatikus tér EA = 65 N / C (lásd. Ábra.). Mi az erő Eb B pontnál?
C3. Egy homogén elektromos térerősség vektort mutat függőlegesen felfelé, lógó labda súlya 10 g, és az adag 5 mC. Amikor a mező ki van kapcsolva a szálfeszítő erő két alkalommal növekszik. Adjuk térerősség.